How I Built a Neural Network from Scratch Without Losing My Mind

(just a quick heads up, this is not meant to be a coding tutorial but a way to visualize neural networks using linear algebra )

After learning about neural networks from various tutorials and lectures, I decided to build one from scratch to understand the inner workings. However, a few days into the project, I found myself drowning in nested for-loops and struggling to keep track of the numerous variables involved in forward and backward propagation.

That's when I had a thought: representing inputs and weights as matrices and using matrix transformations for propagation could simplify everything significantly. This approach would make the code easier to understand, visualize, and maintain.

The Forward Pass: Simplifying with Matrices

I started by rewriting the forward pass using matrices. Instead of looping through each input and weight, I realized I could express the entire layer operation as a single matrix multiplication:

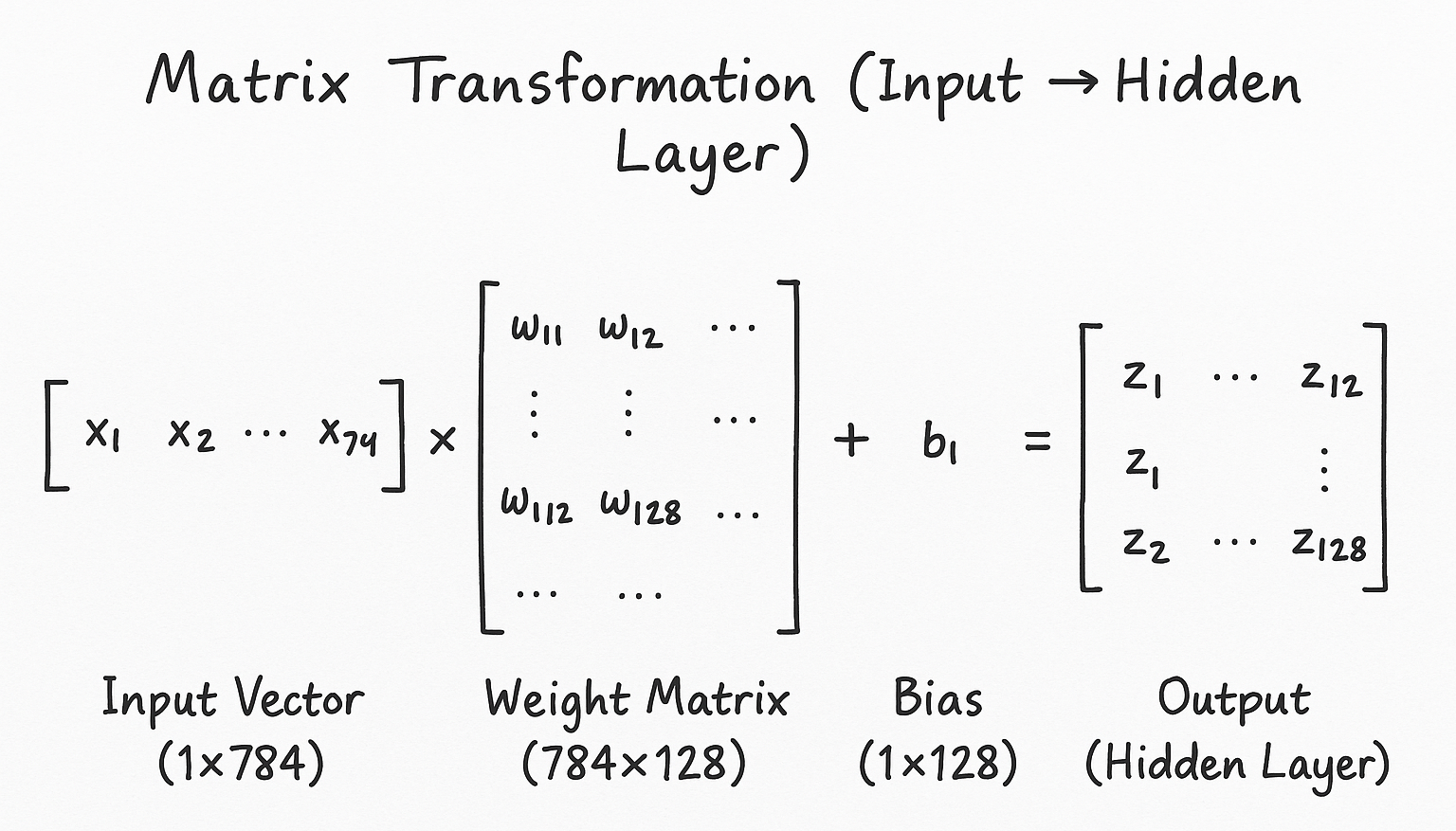
Notice the weight matrix dimensions (784x128). This isn't arbitrary - it's carefully designed to transform our 784-dimensional input into a 128-dimensional representation suitable for the next layer. Essentially, we're performing a linear transformation of the input space.

Backward Pass: Gradient Updates Made Manageable

The backward pass was initially the most challenging part. But with matrices, gradient calculations became surprisingly manageable. Lets assume we are using mean squared loss, then derivating it with respect to weights looks like this:

The equation finally boils down to multiplying derivative of loss fucntion with input matrix X

Also, the matrix operations handle all samples simultaneously, eliminating per-sample loops. This is where the true power of matrix notation shines.

Building the Full Network: MNIST Digit Recognition

With these insights, I built a 3-layer neural network for MNIST digit recognition:

• Input layer (784 neurons)
• Hidden layer (128 neurons with ReLU activation)
• Output layer (10 neurons with Softmax)
• Cross-entropy loss function

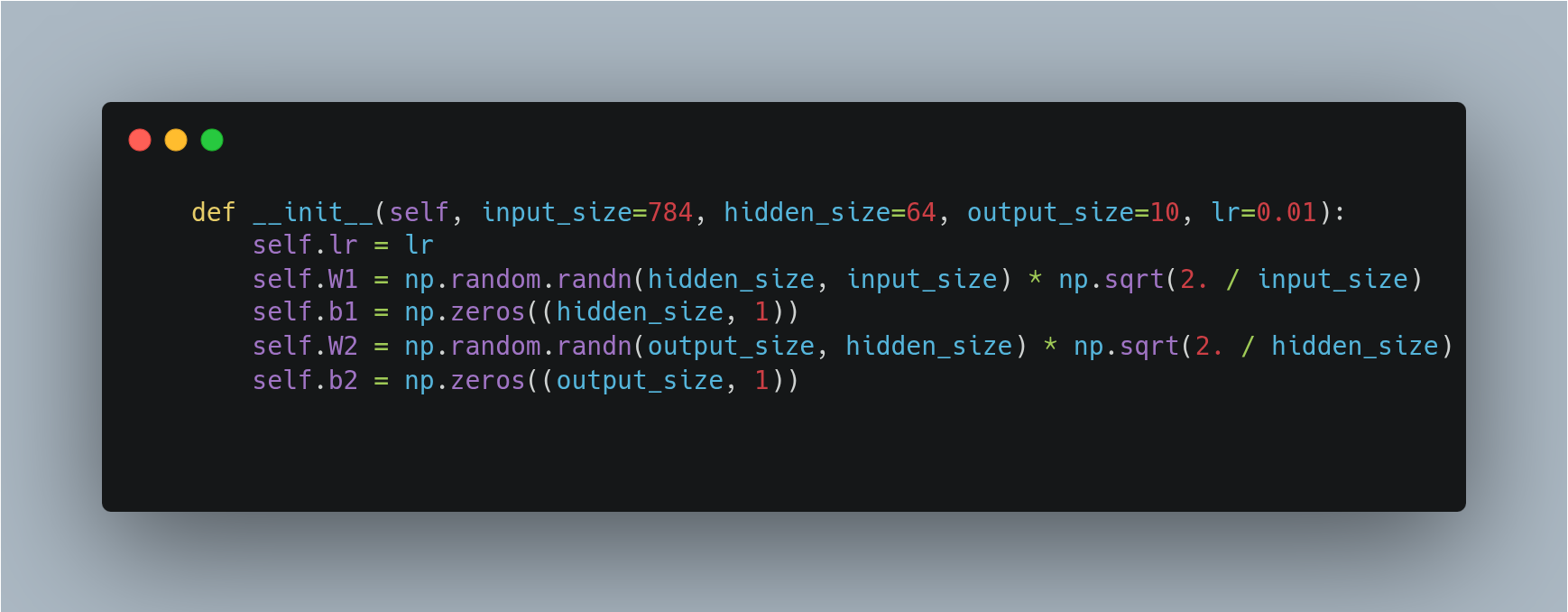
1. The code starts off by initializing weights and bias matrices

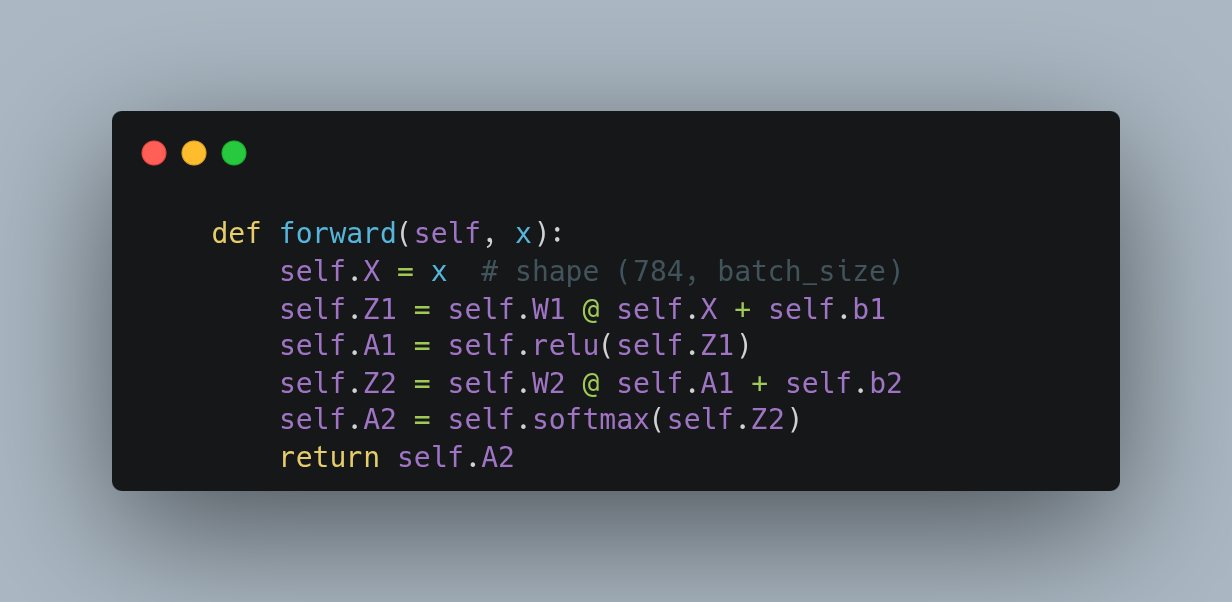
2. Then I wrote the forward pass equations

3. Next challenge was to find derivative of loss function i.e. cross entropy loss function with respect to weights. This is how the derivation looks like (nothing fancy, simple plain calculas)

4. Now writing the backward pass function was prettty easy as derivative of cross entropy loss function boils down to a simple equaltion [y_pred - y_true] *X

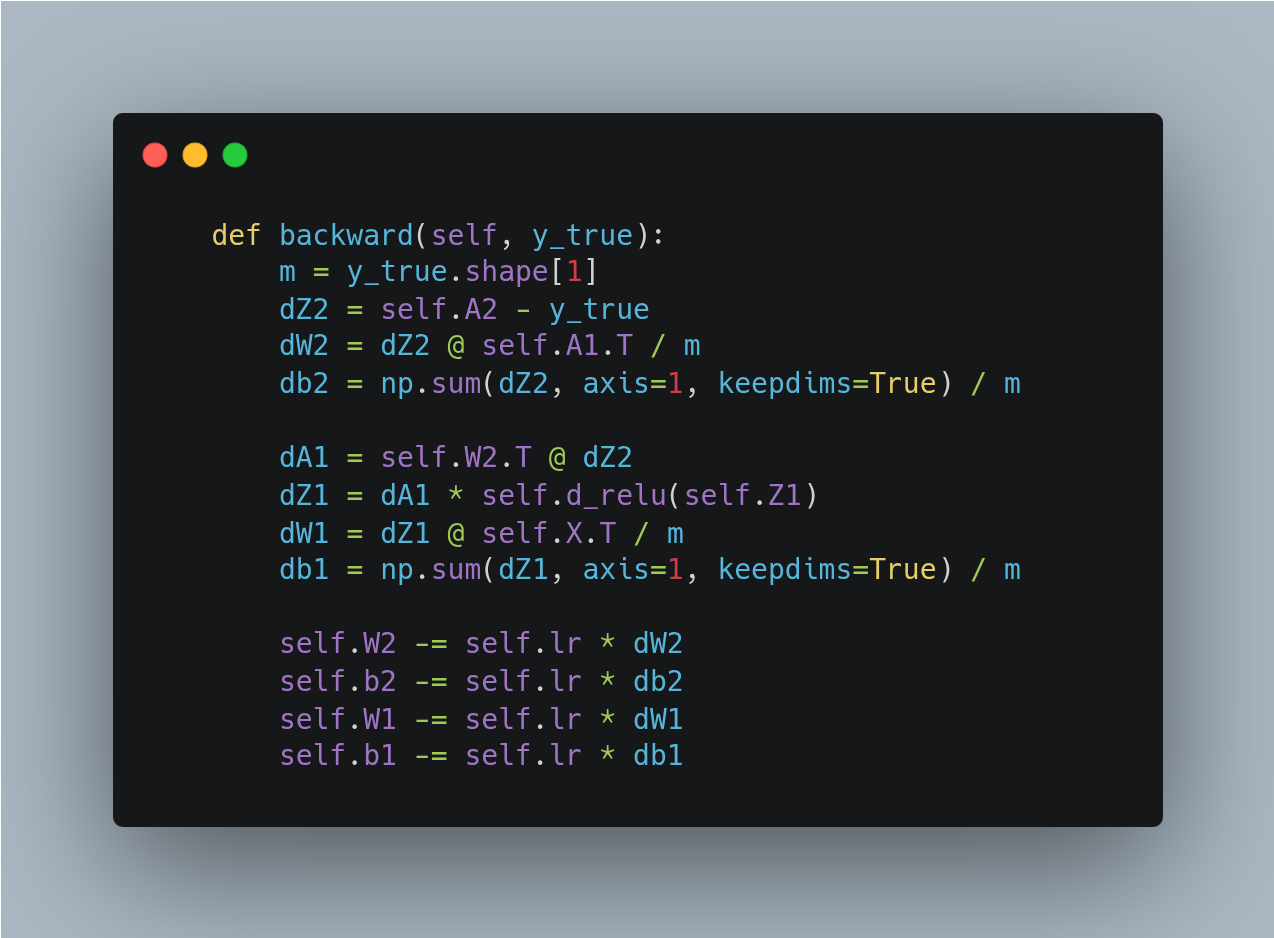
5. Altough it wasn't about getting good accuracy the network stil performs well

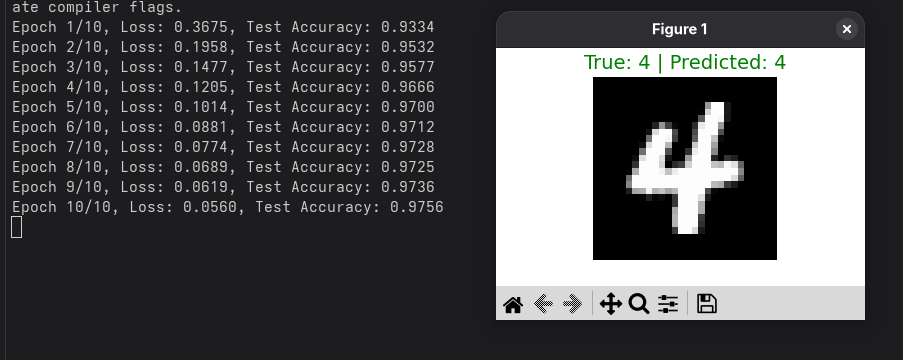
(turns out you cannot escape writing training and testing epochs)

I hope you gained some good insights from this, have a good day!